Answer
The growth rate of the function is 0.07
Solution
We are given a growth function Q(t) defined by:
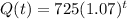
- We are required to find the growth rate of the function.
- The growth rate of the function and the growth factor of the function share a relationship given below:
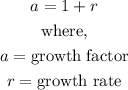
- We know that the growth factor is 1.07, thus, we can find the growth rate as follows:
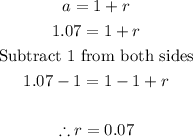
Final Answer
The growth rate of the function is 0.07