Explanation :
It is given that :
Initial velocity,

Launching angle,

The motion followed by this object is called as its projectile motion.
the horizontal component is given by:
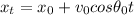 .......(1)
.......(1)
Put all values in equation (1)
For t = 0,

For t = 1 s,

For t = 2 s,
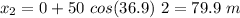
For t = 3 s,
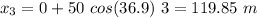
For t = 4 s,
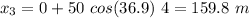
For t = 5 s,
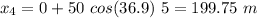
For t = 6 s,
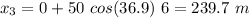
Hence, this is the required solution.