Answer:
The correct option is B.
Explanation:
We need to find how many times larger is
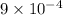 than
than
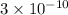 .
.
Let
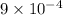 is x times larger than
is x times larger than
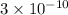 .
.
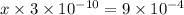
Divide
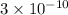 on both sides.
on both sides.
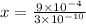
It can be written as
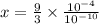
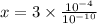
Using quotient property of exponent, we get
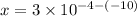
![[\because (a^m)/(a^n)=a^(m-n)]](https://img.qammunity.org/2018/formulas/mathematics/high-school/35suax2b46qzu7syupgh92txkagx8jnbpn.png)
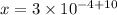
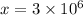
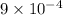 is
is
 times larger than
times larger than
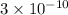 .
.
Therefore the correct option is B.