For this question, we'll need the vertex form of a parabola, which, for a quadratic function, is:

where (h,k) is the vertex of the parabola. In this case, our parabola is opening horizontally to the right, so we need to swap the x and y in our equation. We have:
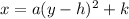
We've been given a the coordinates of the vertex (-4,-1) as well as the coordinates for a point on the parabola (2,0), so we can substitute in the values from both of these coordinates to easily solve for a, the coefficient of the squared term.

So, the coefficient of the squared term for this parabola is 6.