Question

PLEASE HELP!!! What is the product in simplest form? State any restrictions on the variable. z^2/z+1 times z^2+3z+2/z^2+3z

Answer 1

z^2 - z^2+3z+2 ------------------------- z+1 z(z+3) z(z+1)(z+3) is the lcd z^2(z^2+3z)- (z+2)(z+1)(z+1) --------------------------------------... z(z+1)(z+3) z^4+3z^3- (z^2+3z+2)(z+1) z^2+3z+2 z+1 ---------------- z^2+3z+2 z^3+3z^2+2z ------------------------- z^3+4z^2+5z+2 z^4+3z^3-z^3-4z^2-5z-2 ans . z^4+2z^3-4z^2-5z-2 ------------------------------------- z(z+1)(z+3) z ≠0, -1 or -3

Answer 2

Hence, the product is:

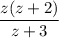`(z(z+2))/(z+3)` such that: z≠ -1,0 and -3.

Explanation:

We are asked to represent the product in the simplest form along with the restrictions applied to z.

We have to evaluate the expression:

`(z^2)/(z+1)* (z^2+3z+2)/(z^2+3z)\\\\=(z^2)/(z+1)* (z^2+3z+2)/(z(z+3))`

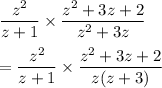
Hence,

z≠ -1,0 and -3.

Since, otherwise the denominator will be equal to zero and hence the product will not be defined.

Now, we know that:

`z^2+3z+2=z^2+2z+z+2\\\\z^2+3z+2=z(z+2)+1(z+2)\\\\z^2+3z+2=(z+1)(z+2)`

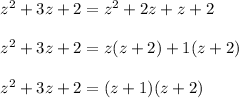
Hence,

`(z^2)/(z+1)* (z^2+3z+2)/(z^2+3z)=(z^2)/(z+1)* ((z+1)(z+2))/(z(z+3))\\\\=(z(z+2))/(z+3)`

( since z and (z+1) term is cancelled as it was same in numerator and denominator)

Hence, the product is:

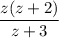`(z(z+2))/(z+3)` such that: z≠ -1,0 and -3.