Question

Using the Rational Root Theorem, what are all the rational roots of the polynomial f(x) = 20x4 + x3 + 8x2 + x – 12?

-4/5 and 3/4

-4/5 and -3/4

-1, -4/5, 3/4 and 1

-1. -4/5, -3/4 and 1

Answer 1

The first option

Explanation:

Right on edg:)

Answer 2

Option 1 is correct.

Explanation:

The given polynomial is

`f(x)=20x^4+x^3+8x^2+x-12`

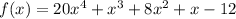
we have to find all the rational roots of the polynomial f(x)

The Rational Root Theorem states that the all possible roots of a polynomial are in the form of a rational number i.e in the form of
`(p)/(q)`

where p is a factor of constant term and q is the factor of coefficient of leading term.

In the given polynomial the constant is -12 and the leading coefficient is 20.

`\text{All possible factor of -12 are }\pm1,\pm2, \pm3, \pm4,\pm6,\pm12`

`\text{All possible factor of 20 are }\pm1,\pm2,\pm4,\pm5,\pm10,\pm20`

So, the all possible rational roots of the given polynomial are,

`\pm1,\pm2, \pm3, \pm4,\pm6,\pm12,\pm(1)/(2),\pm(3)/(2),\pm(1)/(4),\pm(3)/(4),\pm(1)/(10),\pm(1)/(5),\pm(3)/(5),\pm(3)/(10),\pm(2)/(5),\pm(6)/(5),\pm(1)/(20),\pm(3)/(20),\pm(4)/(5),\pm(12)/(5)`

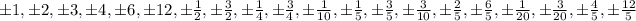
Now, the rational roots of polynomial satisfy the given polynomial

`f(-(4)/(5))=20(-(4)/(5))^4+(-(4)/(5))^3+8(-(4)/(5))^2-(4)/(5)-12=(256)/(625)* 20-(64)/(125)+(128)/(125)-(4)/(5)-12`

`=(1024)/(125)-(64)/(125)+(128)/(25)-(4)/(5)-12`

`=(960)/(125)+(128)/(25)-(4)/(5)-12=12-12=0`

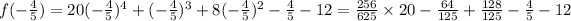
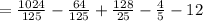
Hence, rational root.

`f((3)/(4))=20((3)/(4))^4+((3)/(4))^3+8((3)/(4))^2+(3)/(4)-12=(405)/(64)+(27)/(64)+(9)/(2)+(3)/(4)-12=0`

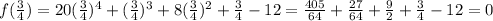
rational root

`f(1)=20(1)^4+(1)^3+8(1)^2+1-12=20+1+8-11=18\\eq 0`

not a rational root.

hence, option 1 is correct