Question

A bag contains 10 green marbles and 4 yellow marbles. If two marbles are chosen at random, one at a time and without replacement, what is the probability of getting two green marbles?

Answer 1

P(green), is 10/14=5/7 because there are 10 green marbles out of the total 14.
P(2nd green), is 9/13 because there are only 9 green marbles and only 13 total marbles. Then you multiply them 5/7 x 9/13 = 35/117

Answer 2

Answer: The required probability of getting two green marbles is 49.45%.

Step-by-step explanation: Given that a bag contains 10 green marbles and 4 yellow marbles. Two marbles are chosen at random, one at a time and without replacement.

We are to find the probability of getting two green marbles.

Let S denote the sample space for the experiment of choosing a marble from the bag and A denote the event of getting a green marble.

The, n(S) = 10 + 4 = 14 and n(A) = 10.

So, the probability of event A will be

`P(A)=(n(A))/(n(S))=(10)/(14)=(5)/(7).`

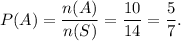
After getting one green marble and not replacing, let S' denote the sample space for the experiment of choosing a marble from the bag

and

let B denote the event of getting another green marble.

Then, n(S') = 14 - 1 = 13 and n(B) = 10 - 1 = 9.

Then, the probability of getting two green marbles is given by

`P\\\\=P(A)* P(B)\\\\=(5)/(7)*(n(B))/(n(S'))\\\\\\=(5)/(7)*(9)/(13)\\\\\\=(45)/(91)*100\%\\\\=49.45\%.`

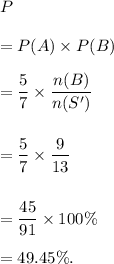
Thus, the required probability of getting two marbles is 49.45%.