Question

*equasion attached*1. The graph opens A. Up B. Down 2. The vertex of the graph is A. (2,5)B(-2,-5)C.(-2,5)3. The axis of symmetry of the graph is A. X=2B. X=-2

Answer 1

We are given the following function:

`y=-(1)/(3)(x+2)^2+5`

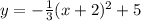
This is a function of the form:

`y=a(x-h)^2+k`

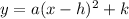
We have that:

`a=-(1)/(3)`

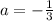
Since the value of "a" is negative this means that the graph opens down.

The vertex of the graph is the point:

`V=(h,k)`

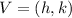
Therefore, the vertex of the function is:

`(h,k)=(-2,5)`

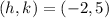
The axis of symmetry of the graph is the x-coordinate of the vertex. Therefore, the axis of symmetry is:

`x=-2`

The graph of the function looks like this: