We are given the following function:
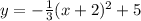
This is a function of the form:
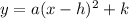
We have that:

Since the value of "a" is negative this means that the graph opens down.
The vertex of the graph is the point:
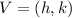
Therefore, the vertex of the function is:
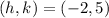
The axis of symmetry of the graph is the x-coordinate of the vertex. Therefore, the axis of symmetry is:

The graph of the function looks like this: