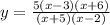It is required to write the equation of a rational function given vertical asymptotes, x-intercepts, and y-intercepts.
Recall that the vertical asymptotes form the factors in the denominator of the function, while the x-intercepts form the factors in the numerator.
Since the vertical asymptotes are x=-5 and x=2, it follows that the factors are (x+5) and (x-2).
Hence, the denominator will be:
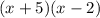
Since the x-intercepts are x=3 and x=-6, then the factors are (x-3) and (x+6).
Hence, part of the numerator is:
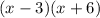
It implies that the rational function takes the form:
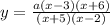
Where a is a constant to be determined.
It is given that the y-intercept is at 9.
Substitute x=0 and y=9 into the equation to calculate the value of a:
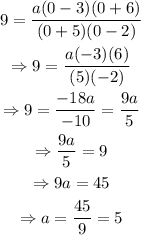
Substitute a=5 back into the function:
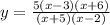
Hence, the required rational function.
The rational function is: