Question

Identify the 7th term of the geometric sequence in which a2 = 324 and a4 = 36

Answer 1

the answer is 4/3 or -4/3

Answer 2

4/3

Explanation:

a2 = 324 and a4 = 36

second term is 324 and fourth term is 36

`a_n= a_1(r)^(n-1)`

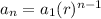
To get second term, replace n with 2

`a_2= a_1(r)^(2-1)`

`a_2= a_1(r)`

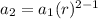
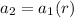
replace a2 with 324

`324= a_1(r)` -----------> equation 1

To get fourth term , replace n with 4

`a_4= a_1(r)^(4-1)`

`a_4= a_1(r)^3`

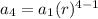
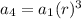
Replace the value

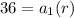`36= a_1(r)` -----------> equation 2

divide second equation by first equation

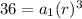`36= a_1(r)^3` divide by
`324= a_1(r)`

1/9 = r^2

take square root on both sides

1/3= r

now we find a1

`324= a_1(r)`

`324= a_1((1)/(3))`

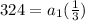
multiply by 3 on both sides

972= a_1

So a1= 972, r= 1/3

now find out 7 term by replacing 'n' with 7

`a_7= 972((1)/(3))^(7-1)`

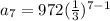
So 7th term is 4/3