Going from step 1 to step 2, the person has factored out x. However, this is incorrect because there is no x to factor from the last term d.
Factoring like this is simply the distributive property in reverse. We can check if we did the factoring right by distributing the outer term x back into the inner terms
Let's multiply the outer x by each of the inner terms (a, b and d)
x times a = ax
x times b = bx
x times d = dx <--- the result should be d and not dx
-----------------------------------------------------------------------------
Here is the proper way to solve for x. We first need to move the d over, which is done by subtracting d from both sides. Once all of the x terms are on one side, we can finally factor out the x. Then after that we divide both sides by the quantity (a+b)
k = ax + bx + d
k - d = ax + bx + d - d
k - d = ax + bx
k - d = x(a + b)
(k - d)/(a + b) = x(a + b)/(a + b)
(k - d)/(a + b) = x
x = (k - d)/(a + b)
The final answer is
x = (k - d)/(a + b)
which can be written as
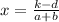
If you choose to use the first option, then make sure you use parenthesis as shown. The parenthesis are important to make sure that you divide all of "k-d" over all of "a+b" as one big fraction.