Question

Given that the points (-1, 6), (3, 6), (3, 1), and (-1, 1) are vertices of a rectangle, how much shorter is the width than the length?

Answer 1

check the picture below, you can pretty much count the units off the grid.

Answer 2

1 unit shorter

Explanation:

By plotting the given points in the coordinate plane,

We get a rectangle ABCD having vertices,

A(-1,6), B (3,6), C (3,1), D (-1,1)

By the distance formula,

Shorter side or width of the rectangle,

`AB=√((3-(-1))^2+(6-6)^2)=√(4^2+0)=4\text{ unit}`

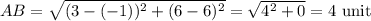
Longer side or length of the rectangle,

`BC=√((3-3)^2+(1-6)^2)=√(5^2)=5\text{ unit}`

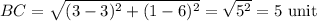
The difference between length and width,

`BC - AB = 5 - 4 = 1\text{ unit}`

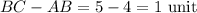
Hence, the width of rectangle is 1 unit less than the length.