Question

please help area of triangle: law of sines!! other tutors couldn’t solve so they referred me to different people!

Answer 1

In order to solve this exercise we must apply:

1) The Law of Sines

2) Heron's formula:

Now, we take the triangle of our problem and we put names to the sides and angles:

Sides of the triangle:

a = XY = ?

b = WY = 15 mi

c = XW = ?

Angles of the triangle:

α = ∠XWY = 180° - 112° - 27° = 41°

β = ∠WXY = 112°

γ = ∠XYW = 27°

Where in order to find α we took in account that the inner angles of a triangle sums 180°.

------------------------

With Heron's formula we see that we can obtain the area of the triangle but we need the lenghts a, b and c of the sides. So we will use the Law of Sines to determine each side and then with that data we will calculate the area using Heron's formula.

1) We calculate the lenghts of a and c, we apply the Law of Sines with the data that we know.

`\begin{gathered} (a)/(\sin\alpha)=(b)/(\sin\beta) \\ a=(\sin\alpha)/(\sin\beta)\cdot b \\ a=(\sin(41^(\circ)))/(\sin(112^(\circ)))\cdot15\cong10.61374 \end{gathered}`

`\begin{gathered} (c)/(\sin\gamma)=(b)/(\sin\beta) \\ c=(\sin\gamma)/(\sin\beta)\cdot b \\ c=\frac{\sin(27^(\circ))}{\sin(112^(\circ)^{})}\cdot15\cong7.34467 \end{gathered}`

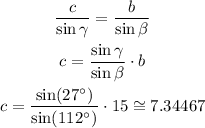
Now we know the length of the three sides:

a ≅ 10.61374

b = 15

c ≅ 7.34467

2) We calculate the semi-perimeter of the triangle:

`\begin{gathered} s=(a+b+c)/(2) \\ s\cong(10.61374+15+7.34467)/(2) \\ s\cong16.4792 \end{gathered}`

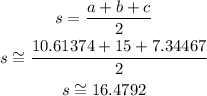
Now, using the semi-perimeter, the length of the sides and Heron's formula we calculate the area of the triangle:

`\begin{gathered} A=\sqrt[]{s\cdot(s-a)\cdot(s-b)\cdot(s-c)} \\ A\cong36.1390\cong36.1 \end{gathered}`

Answer

The area of the triangle △WXY to the nearest tenth is 36.1 mi².