The quadratic equation is given as,
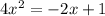
Consider that the standard quadratic equation is given by,
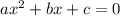
Writing the equation in standard form,
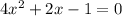
Comparing the coefficients,
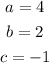
The discriminant of a quadratic equation is given by,
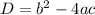
Consider the following three cases for the nature of roots of any quadratic equation,
• Real and distinct roots:
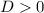
• Real and equal roots (only one real root):
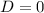
• Imaginary roots (Non-real roots):
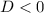
Now, obtain the discriminant for the given quadratic equation as,
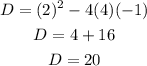
As the discriminant of the quadratic equation comes out to be positive, this corresponds to the first case when the roots/solutions are real and distinct.
Thus, it can be concluded that the given quadratic equation has two real and distinct roots.
Therefore, 1st option is the correct choice.
Consider that the solutions or roots of a quadratic equation are given by the formula,
![x=\frac{-b\pm\sqrt[]{D}}{2a}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/o2o4332ao3bw7vjud1pg.png)
Substitute the values corresponding to the given quadratic equation,
![\begin{gathered} x=\frac{-(2)\pm\sqrt[]{20}}{2(4)} \\ x=\frac{-2\pm\sqrt[]{2^2\cdot5}}{8} \\ x=\frac{-2\pm2\sqrt[]{5}}{8} \\ x=\frac{-1\pm\sqrt[]{5}}{4} \\ x=\frac{-1+\sqrt[]{5}}{4}\text{ or }x=\frac{-1-\sqrt[]{5}}{4} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/unsm5don6jg7vf6pkoi8.png)
Thus, the roots of the given quadratic equation are,
![\frac{-1+\sqrt[]{5}}{4}\text{ and }\frac{-1-\sqrt[]{5}}{4}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/4vr95n18la6u0u7ep1b0.png)