Question

Sarah polled 40 randomly selected students at her high school and found that 20% ( = 0.2) are happy with the quality of the cafeteria food. With a desired confidence level of 99%, which has a corresponding z*-score of 2.58, what is the approximate margin of error of Sarah’s poll? Remember, the margin of error, E, can be determined using the formula E = z*

Answer 1

The answer is D: 16%

Explanation:

I just took the test.

Answer 2

Given:
n = 40, sample size
Confidence level = 99% => z* = 2.58

`\hat{p} = 20\%=0.2`, sample proportion.

By definition, the margin of error is

`z^(*) \sqrt{ \frac{\hat{p}(1-\hat{p})}{n} } = 2.58 \sqrt{ ((0.2)(0.8))/(40) }= 0.1632`

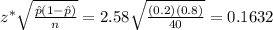
Answer:
According to Sarah's poll, she can conclude with 99% confidence level that 20% of the high school population is happy with the quality of the cafeteria food, with a margin of error of +/- 16.3%.