The model function is
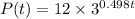
where t is the time in days and P(t) is the population along the time.
Question a.
Initially, at t=0, the population is
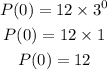
that is, there was 12 fruits.
Question b.
After t=6, we have
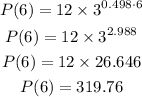
that is, by rounding up, there will be 320 fruits.
Question c.
In this case, we have P(t)=8 000, then we have
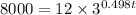
If we move 12 to the left hand side, we get
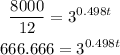
By applying natural logarithms on both sides, we obtain
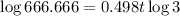
then, t is equal to
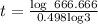
therefore, t is
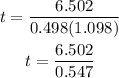
and t is equal to 11.88 days. By rounding up, t=12 days.
Question d.
The number of fruits