Question

Two chemical plants, one in Macon and one in Jonesboro, produce three types of fertilizer: LP, MP, and HP. The Macon plant produces 1 ton of LP, 2 tons of MP, and 3 tons of HP per hour. The Jonesboro plant produces 1 ton of LP, 5 tons of MP, and 1 ton of HP. On any given day, the company needs to produce atleast 100 tons of LP, 260 tons of MP, and 180 tons of HP. If it costs $600 per hour to run the Macon plant, and $1000 an hour to run the Jonesboro plant, how many hours should each plant be run in order to minimize cost?-I'm not sure what the correct variables are and how to make the right equations I need to graph. I need to solve this problem by creating equations like 6x+7y>100. Then once I have them I need to graph all of then and shade the line based on the inequality sign. If someone could help that would be great!

Answer 1

We have a linear optimization problem.

We have two plants with different capacity for each type of fertilizer. Each hour, the plant can produce a mix of the products.

Each plant has an associated cost per hour of operation.

Let:

J: the number of operation hours of the Jonesboro plant

M: the number of operation hours of the Macon plant

We can write the total production for the LP fertilizer as:

`\begin{gathered} 1\cdot J+1\cdot M\ge100 \\ J+M\ge100 \end{gathered}`

Each plant produces one ton per hour, and the total production of both plants togheter has to be 100 tons or more.

For the MP fertilizer, we can similarly write:

`5J+2M\ge260`

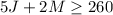
For the HP fertilizer, we can write:

`J+3M\ge180`

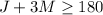
We have the equations of the restrictions:

`\begin{gathered} J+M\ge100 \\ 5J+2M\ge260 \\ J+3M\ge180 \end{gathered}`

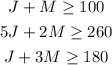
The objective function is the cost function, that have to be minimized:

`1000J+600M`

We can graph the restrictions as:

(J is written as x and M as y)

Now we can graph the objective function, and minimize satisfying all the restrictions:

We can see that the minimization happens when the MP and HP restrictions meet (both restrictions are "saturated").

Then, we can write:

`\begin{gathered} 5J+2M=260 \\ J+3M=180\longrightarrow J=180-3M \\ \\ 5(180-3M)+2M=260 \\ 900-15M+2M=260 \\ 900-13M=260 \\ 13M=900-260 \\ 13M=640 \\ M=(640)/(13)\approx49.231 \\ \\ J=180-3M=180-3(49.231)=180-147.693=32.307 \end{gathered}`

The cost is:

`1000J+600M=1000\cdot32.307+600\cdot49.231=32,307+29,538.60=61,845.60`

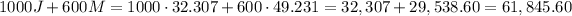
The combination that minimize the cost is:

Hours of Jonesboro plant: 32.307 hours

Hours of Macon plant: 49.231 hours.

Total cost: $ 61,845.60