Answer:
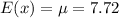
Explanations:
The formula for finding the expected value of a probability distribution is expressed as:
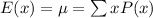
Substituting the values in the table into the formula will give:
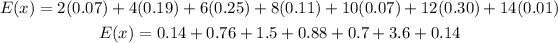
Taking the resulting sum of to get the expected value;
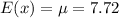
Hence the expected value of the probability distribution of the discrete random variable X is 7.72