Question

What is the area of a parallelogram whose vertices are A(−1, 12) , B(13, 12) , C(2, −5) , and D(−12, −5) ?

Answer 1

AB = 14, that is our base length, then the height is the 12 to -5, or 17 in length, then multiply those 2 numbers 17 x 14, to get 238

Answer 2

Answer: The area of the parallelogram with the given vertices=238 square units.

Explanation:

Let CD be the base of the parallelogram ABCD is given by distance formula

CD=
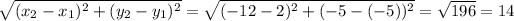`√((x_2-x_1)^2+(y_2-y_1)^2) =√((-12-2)^2+(-5-(-5))^2) =√(196) =14`units[or you can count distance by using graph as ordinates of C and D are same to we can count the distance of x from C to D]

Now consider P a point on CD such that AP become the height of the parallelogram which is given by (from the graph attached)=17 [as abscissa of P and A are same to we can count the distance of y from A to P]

Area of parallelogram = base × height=14×17=238 square units.