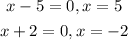Question

Factoring and quadratic Equations.The solution of quadratic equations helps in solving some practical problems. What are the 7 recommended strategy steps for solving these problems?

Answer 1

Given: Factoring and quadratic equation

To Determine: 7 recommended strategy steps for solving these problems

Solution

The 7 recommended strategy steps for solving these problems are:

1. Completing the square.

2. Quadratic formula.

3. AC method (various variants)

4. Guessing (perhaps helped by rational roots theorem)

5. Sum of coefficients shortcut.

6. Pattern recognition of perfect square trinomials.

7. Graphical method

To solve an quadratic equation using factoring :

1 . Transform the equation using standard form in which one side is zero. e.g.

`\begin{gathered} x^2-3x=10 \\ x^2-3x-10=0 \end{gathered}`

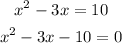
2 . Factor the non-zero side.

`Factor:x^2-3x-10`

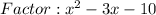
3. Determine the product

`product=x^2*-10=-10x^2`

4. Determine the sum

`-3x`

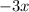
5. Determine two product factors of the the product that if added to each other wuld give the sum

`\begin{gathered} -10x^2 \\ -5x*2x=-10x^2 \\ -5x+2x=-3x \end{gathered}`

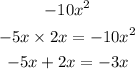
So, we have

`\begin{gathered} x^2-5x+2x-10 \\ x(x-5)+2(x-5)=0 \\ (x-5)(x+2)=0 \end{gathered}`

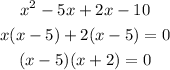
6 . Set each factor to zero (Remember: a product of factors is zero if and only if one or more of the factors is zero).

`x-5=0,OR,x+2=0`

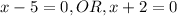
7 . Solve each resulting equation

`\begin{gathered} x-5=0,x=5 \\ x+2=0,x=-2 \end{gathered}`