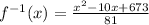Question

The functionx > or equal to 8f(x) = -9/x – 8+5has an inverse f-1(x) defined on the domain x < or equal to 5. Find the inverse.

Answer 1

Here we have the function:

`f(x)=-9\sqrt[]{x-8}+5;x>8`

We're going to find the inverse function;

`f^(-1)(x)`

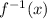
For this, we're going to solve the following equation for x: (Let f(x) be y).

`y=-9\sqrt[]{x-8}+5`

We could square both sides as follows:

`\begin{gathered} y-5=-9\sqrt[]{x-8} \\ (y-5)^2=(-9\sqrt[]{x-8)}^2) \end{gathered}`

Now, we could rewrite:

`\begin{gathered} y^2-10y+25=81(x-8) \\ y^2-10y+25=81x-648 \end{gathered}`

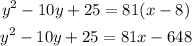
And then solve for x:

`\begin{gathered} y^2-10y+25=81x-648 \\ y^2-10y+25+648=81x \\ y^2-10y+673=81x \\ (y^2-10y+673)/(81)=x \end{gathered}`

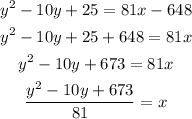
Finally, we can write:

`f^(-1)(x)=(x^2-10x+673)/(81)`