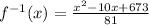Here we have the function:
![f(x)=-9\sqrt[]{x-8}+5;x>8](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/cyq27hk1ewepg1s0tz08.png)
We're going to find the inverse function;
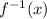
For this, we're going to solve the following equation for x: (Let f(x) be y).
![y=-9\sqrt[]{x-8}+5](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/7t84i28gwmtjljcyz31x.png)
We could square both sides as follows:
![\begin{gathered} y-5=-9\sqrt[]{x-8} \\ (y-5)^2=(-9\sqrt[]{x-8)}^2) \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/s5re3jusuwdmzxissp6r.png)
Now, we could rewrite:
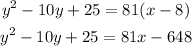
And then solve for x:
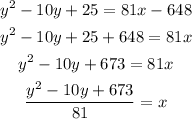
Finally, we can write: