Question

this is a 3 part question10) A 3.5-inch floppy disk in a computer rotates with a period of 2.00x10^-1s. What are (a) the angular speed of the disk and (b) the linear speed of a point on the rim of the disk? (c) Does a point near the center of the disk have an angular speed that is greater than, less than, or the same as the angular speed found in part (a)? Explain. (Note: A 3.5-inch floppy disk is 3.5 inches in diameter.)

Answer 1

(a) 10π rad/s

(b) 58.98 in/s

(c) A point near the center of the disk have an angular speed that is the same as the angular speed found in part (a).

Step-by-step explanation:

Part (a)

The angular speed w can be calculated as

`w=(2\pi)/(T)`

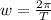
Where T is the period. So, replacing T = 2.00 x 10^-1 s, we get

`w=(2\pi)/(2.00*10^(-1)s)=10\pi\text{ rad/s}`

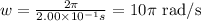
Then, the angular speed of the disk is 10π rad/s

Part (b)

The linear speed v is equal to

`v=wr`

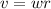
Where r is the radius. The radius is half the diameter, so the radius of a point on the rim of the disk will be 3.5 in/2 = 1.75 in. Then, the linear speed will be

`v=(10\pi\text{ rad/s)(1.75 in) = 54.98 in/s}`

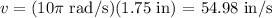
Therefore, the linear speed of a point on the rim of the disk is 54.98 in/s

Part(c)

The angular speed is equal to the angular displacement divided by the time. Since a point near to the centar have the same angular displacement as a point on the rim of the disk, the angular speed will be the same.

So, the answer is a point near the center of the disk have an angular speed that is the same as the angular speed found in part (a).

Therefore, the answers are

(a) 10π rad/s

(b) 58.98 in/s

(c) A point near the center of the disk have an angular speed that is the same as the angular speed found in part (a).