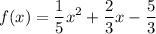Question

If 4f(x)+f(5-x)=x2

What is f(x)?

Answer 1

We are given that
`4f(x)+f(5-x)=x^2`.

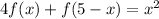
Substitute x with 5-x, then the above equation becomes:


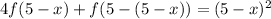
`4f(5-x)+f(5-(5-x))=(5-x)^2`, that is


`4f(5-x)+f(x)=(5-x)^2`


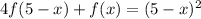
So, we have the following system of equations:

i)
`4f(x)+f(5-x)=x^2`
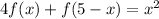
ii)
`4f(5-x)+f(x)=(5-x)^2`

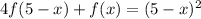
multiply the first equation by -4, so that we eliminate f(5-x)'s

i)
`-16f(x)-4f(5-x)=-4x^2`
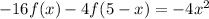
ii)
`4f(5-x)+f(x)=(5-x)^2`

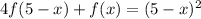
adding the 2 equations side by side we have:


`-15f(x)=-4x^2+(5-x)^2`

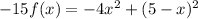
expanding the binomial, and collecting same terms we have:


`-15f(x)=-4x^2+(25-10x+x^2)`


`-15f(x)=-3x^2-10x+25`

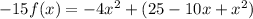
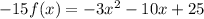
dividing by -5:


`3f(x)=(3)/(5)x^2+2x-5`

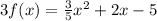
dividing by 3:


`\displaystyle{f(x)= (1)/(5)x^2+ (2)/(3)x-(5)/(3)`


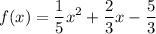
Answer:
`\displaystyle{f(x)= (1)/(5)x^2+ (2)/(3)x-(5)/(3)`