Question

Find the minimum and maximum of f(x,y,z)=x^2+y^2+z^2 subject to two constraints, x+2y+z=4 and x-y=8.

Answer 1

The Lagrangian for this function and the given constraints is


`L(x,y,z,\lambda_1,\lambda_2)=x^2+y^2+z^2+\lambda_1(x+2y+z-4)+\lambda_2(x-y-8)`

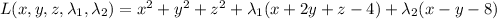
which has partial derivatives (set equal to 0) satisfying


`\begin{cases}L_x=2x+\lambda_1+\lambda_2=0\\L_y=2y+2\lambda_1-\lambda_2=0\\L_z=2z+\lambda_1=0\\L_(\lambda_1)=x+2y+z-4=0\\L_(\lambda_2)=x-y-8=0\end{cases}`

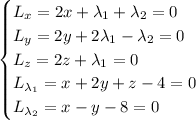
This is a fairly standard linear system. Solving yields Lagrange multipliers of
`\lambda_1=-(32)/(11)` and
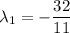
`\lambda_2=-(104)/(11)`, and at the same time we find only one critical point at
`(x,y,z)=\left((68)/(11),-(20)/(11),(16)/(11)\right)`.

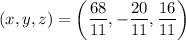
Check the Hessian for
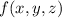
`f(x,y,z)`, given by





`\mathbf H` is positive definite, since
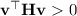
`\mathbf v^\top\mathbf{Hv}>0` for any vector
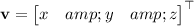
`\mathbf v=\begin{bmatrix}x&y&z\end{bmatrix}^\top`, which means
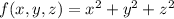
`f(x,y,z)=x^2+y^2+z^2` attains a minimum value of
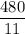
`(480)/(11)` at
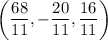
`\left((68)/(11),-(20)/(11),(16)/(11)\right)`. There is no maximum over the given constraints.