Question

In the problem, angle c is a right angle. Solve the triangle rounding answers to the nearest tenth.c=13 in, m angle B= 35

Answer 1

Solve the following triangle

We are given two of the interior angles, c=90°, and b=35°. The third angle must have a measure such that the sum of them is 180°, thus:

a = 180° - 90° - 35° = 55°

Now calculate the length of BC by using the cosine ratio:

`\cos 35^o=\frac{\text{adjacent side}}{hypotenuse}`

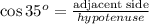
Substituting;

`\cos 35^o=(BC)/(13)`

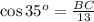
Solving for BC:

BC = 13 cos 35°

Calculating:

BC = 13 * 0.81915

BC = 10.6 in (to the nearest tenth)

For the length of AC, we use the sine ratio

`\sin 35^o=\frac{\text{opposite side}}{hypotenuse}`

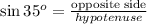
Substituting:

`\sin 35^o=(AC)/(13)`

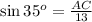
Solving for AC:

AC = 13 sin 35°

Calculating:

AC= 13 * 0.5736

AC = 7.4 in

Summary:

Angle A = 55°

Side BC = 10.6 in

Side AC = 7.4 in