Question

Explain how it to use linear factors to determine the equation of a polynomial function

Answer 1

Since linear factors can be written as (x-a)*(x-b) with a and b as the solutions, we can do it in two ways. First, we can use the quadratic equation. In an equation ax²+bx+c=0, the solutions are

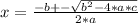
`x= \frac{-b+- \sqrt{ b^(2)-4*a*c} }{2*a}` with the +- meaning that you can have one solution (a) by adding and (b) by subtracting.

Next, in ax²+bx+c=0, we want to add b up to have dx+zx=bx as well as (d*z)=(c*a). For example, in 6x²+2x-4, we have 6*-4=-24. We have to find 2 numbers that add up to 2 but multiply to 24 - -4 and 6 work. Therefore, we have 6x²+6x-4x-4. Factoring it out, we have 6x(x+1)-4(x+1). Since x+1 is the same in both, we have the equation being (6x-4)(x+1) as the factorization