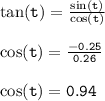Answer:
cos(t) = 0.94
Explanation:
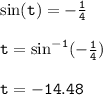
- therefore;
- A circle has four trigonometric quadrants;
- quadrant I → All angles are positive
- quadrant II → only sine angles are positive (180 - x)
- quadrant III → only tangent angles are positive (180 + x)
- quadrant IV → only cosine angles are positive (360 - x)
In the quadrant III, sine angles are negative;
- Since t is in the third quadrant;
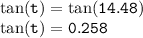
- Therefore;