Question

The polynomial equation x^3-4x^2+2x+10=x^2-5x-3 has complex roots 3+2i What is the other root? Use a graphing calculator and a system of equations.

a –3
b –1
c 3
d 10

Answer 1

The other root would be (B) -1

Answer 2

The correct option is b.

Explanation:

The given expression is

`x^3-4x^2+2x+10=x^2-5x-3`

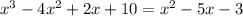
Simplify the equation.

`x^3-4x^2+2x+10-x^2+5x+3=0`

`x^3-5x^2+7x+13=0`

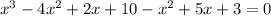
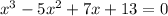
It is given that 3+2i is a root of the equation and (x-3-2i) is a factor.

By complex conjugate root theorem if a+ib is a root of an equation then a-ib must be the root of the equation.

It means 3-2i is a root of the equation and (x-3+2i) is a factor.

`(x-3-2i)(x-3+2i)=(x-3)^2-(2i)^2=x^2-6x+9+4=x^2-6x+13`

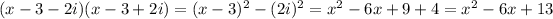
Divide
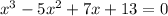`x^3-5x^2+7x+13=0` by
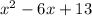`x^2-6x+13`, to find the remaining factor.

By the long division method, the quotient is (x+1) and remainder is 0. It means (x+1) is a remaining factor of the given equation. Equate each factor equal to 0, to find the remaining roots.

`x+1=0`

`x=-1`

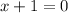
Therefore the correct option is b.