Finding the cube root of each expression
Expression A:
![\sqrt[3]{-8x^(21)y^(8)}](https://img.qammunity.org/2018/formulas/mathematics/high-school/vbtsm3yerh8d1gn9lo0ayzrueit1p7y06q.png)
![\sqrt[3]{-8}](https://img.qammunity.org/2018/formulas/mathematics/high-school/4iw50eb7t27i2u2o8fevz2xnnog70n9qyt.png)
![\sqrt[3]{x^(21)[tex] \sqrt[3]{y^8}]()
} [/tex]
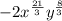
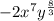
the term
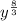
is not a perfect cube, therefore expression A is not a perfect cube.
--------------------------------------------------------------------------------------------------------------
Expression B
![\sqrt[3]{-64x^(64)y^(64)}](https://img.qammunity.org/2018/formulas/mathematics/high-school/lrskahv7v2rt5zmtuiv1dxj2u8g7hub509.png)
![\sqrt[3]{-64} \sqrt[3]{x^(64)} \sqrt[3]{y^(64)}](https://img.qammunity.org/2018/formulas/mathematics/high-school/5rkg7jcaddcqhtd2yj5vp4k5r866and9f8.png)
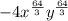
The term
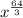
and
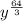
are not perfect cube because 64/3 doesn't give whole number
----------------------------------------------------------------------------------------------------------------
Expression C
![\sqrt[3] {-125x^9y^(20)}](https://img.qammunity.org/2018/formulas/mathematics/high-school/15ezsp1dzkdscgar0xmdhs7n0vegtth6xp.png)
![\sqrt[3]{-125} \sqrt[3]{x^9} \sqrt[3] {y^(20)}](https://img.qammunity.org/2018/formulas/mathematics/high-school/cwkglbkjrzm4dkow4cqgup3i4xpyi2rell.png)
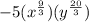
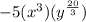
The term
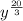
are not perfect cube because 20/3 doesn't give whole number
---------------------------------------------------------------------------------------------------------------
Expression D
![\sqrt[3]{ -216 x^(9) y^(18) }](https://img.qammunity.org/2018/formulas/mathematics/high-school/xayal2k8p0vceleom3w9e805acbdfpmux0.png)
![\sqrt[3]{-216} \sqrt[3]{x^9} \sqrt[3]{y^(18)}](https://img.qammunity.org/2018/formulas/mathematics/high-school/lhkhfh6qzxwxbahht13mtd96azbgwg6rxz.png)
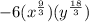
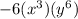
All terms are perfect cubes
ANSWER: OPTION D