Solution:
A linear relationship is expressed as

let
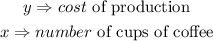
Given that the cost to produce 150 cups of coffee is $80, this implies that

if the cost to produce 300 cups is $155, this implies that
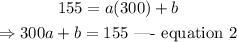
A) write a linear equation that expresses the cost why in terms of the number of cups of coffee x
To express the linear equation, we solve for a and b simultaneously.
By the method of elimination,
step 1: Subtract equation 1 from equation 2.
Thus,

step 2: Substitute the obtained value of a into equation 1.
Thus, from equation 1,
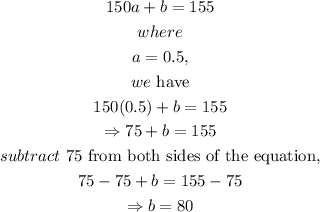
Step 3: Substitute the value of a and b into equation (*).
Thus, the linear equation is expressed as
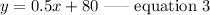
B) Number of cups produced if the cost of production is 210.
To evaluate the number of cups, substitute the value of 210 for y in equation 3.
Thus, from equation 3,

Hence, the number of cups of coffee produced is 260.