Question

The manager of a restaurant found that the cost to produce 150 cups of coffee is $80 while the cost to produce 300 cups is $155 assume the relationship between the cost Y to produce X cups of coffee is linear a. write a linear equation that expresses the cost why in terms of the number of cops of coffee XB. how many cups of coffee are produced in the cost of production is 210

Answer 1

A linear relationship is expressed as

`y=ax+b\text{ ----- equation \lparen *\rparen}`

let

`\begin{gathered} y\Rightarrow cost\text{ of production} \\ x\Rightarrow number\text{ of cups of coffee} \end{gathered}`

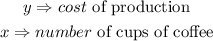
Given that the cost to produce 150 cups of coffee is $80, this implies that

`\begin{gathered} 80=a(150)+b \\ \Rightarrow150a+b=80\text{ ---- equation 1} \end{gathered}`

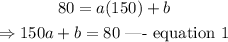
if the cost to produce 300 cups is $155, this implies that

`\begin{gathered} 155=a(300)+b \\ \Rightarrow300a+b=155\text{ ---- equation 2} \end{gathered}`

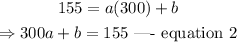
A) write a linear equation that expresses the cost why in terms of the number of cups of coffee x

To express the linear equation, we solve for a and b simultaneously.

By the method of elimination,

step 1: Subtract equation 1 from equation 2.

Thus,

`\begin{gathered} (300a-150a)+(b-b)=(155-80) \\ \Rightarrow150a=75 \\ divide\text{ both sides by the coefficient of a.} \\ the\text{ coefficient of a is 150.} \\ thus, \\ (150a)/(150)=(75)/(150) \\ \Rightarrow a=0.5 \end{gathered}`

step 2: Substitute the obtained value of a into equation 1.

Thus, from equation 1,

`\begin{gathered} 150a+b=155 \\ where \\ a=0.5, \\ we\text{ have} \\ 150(0.5)+b=155 \\ \Rightarrow75+b=155 \\ subtract\text{ 75 from both sides of the equation,} \\ 75-75+b=155-75 \\ \Rightarrow b=80 \end{gathered}`

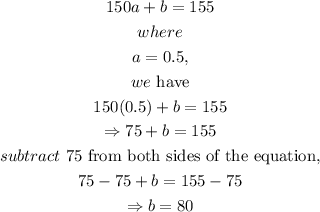
Step 3: Substitute the value of a and b into equation (*).

Thus, the linear equation is expressed as

`y=0.5x+80\text{ ----- equation 3}`

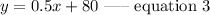
B) Number of cups produced if the cost of production is 210.

To evaluate the number of cups, substitute the value of 210 for y in equation 3.

Thus, from equation 3,

`\begin{gathered} y=0.5x+80 \\ where\text{ y=210} \\ thus, \\ 210=0.5x+80 \\ subtract\text{ 80 from both sides of the equation} \\ 210-80=0.5x+80-80 \\ \Rightarrow130=0.5x \\ divide\text{ both sides by 0.5} \\ (130)/(0.5)=(0.5x)/(0.5) \\ \Rightarrow x=260 \end{gathered}`

Hence, the number of cups of coffee produced is 260.