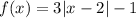Question

Identify the function that has a vertex of (2,-1) and is stretched vertically by a factor of 3.

f(x) = ⅓|x - 2| - 1
f(x) = |x - 2| + 4
f(x) = ⅓|x + 2| - 1
f(x) = 3|x - 2| - 1

Answer 1

f(x) = 3|x - 2| - 1
is the function

Answer 2

`f(x)=3|x-2|-1`

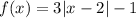
Explanation:

Identify the function that has a vertex of (2,-1) and is stretched vertically by a factor of 3.

The option are absolute function, So the parent function is y=|x|

Vertex form of absolute function is

`y=|x-h|+ k` where (h,k) is the vertex

vertex of (2,-1) h=2, k =-1

the function becomes

`f(x)=|x-2|-1`

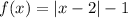
function is stretched vertically by a factor of 3

when f(x) is vertically stretched by a factor of 'a'.We multiply the factor with f(x)

`f(x)=3|x-2|-1`