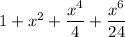Not clear if you're supposed to find a series solution to the ODE, or solve exactly then give the requested terms of the series expansion of the that solution...
The exact solution is easy enough to find. We can separate the variables:


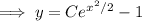
Given that
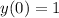
, we have
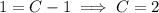
Then recall that
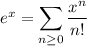
to write the solution as

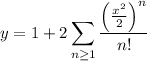
so the first four terms of the series are