Question

If s = {r, u, d} is a set of linearly dependent vectors. if x = 5r + u + d, determine whether t = {r, u, x} is a linearly dependent set

Answer 1

Consider any arbitrary linear combination of the vectors
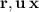
`\mathbf r,\mathbf u\,\mathbf x`. We have


`c_1\mathbf r+c_2\mathbf u+c_3\mathbf x=c_1\mathbf r+c_2\mathbf u+c_3(5\mathbf r+\mathbf u+\mathbf d)`

`=(c_1+5c_3)\mathbf r+(c_2+c_3)\mathbf u+c_3\mathbf d`

`=c_4\mathbf r+c_5\mathbf u+c_6\mathbf d`

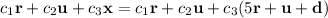
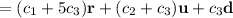
We know
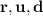
`\mathbf r,\mathbf u,\mathbf d` are linearly dependent, which means there must exist some choice of not all zero constants
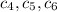
`c_4,c_5,c_6` such that the combination above gives the zero vector. So
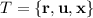
`T=\{\mathbf r,\mathbf u,\mathbf x\}` is a set of linearly dependent vectors.