Question

At the candy store, Sophie filled a bag with 2 2/3 kilograms of candy. 1/4 of the weight of the candy was from chocolate covered pretzels. How much did the chocolate covered pretzels in Sophie’s bag weigh?

Answer 1

The answer is: " ⅔ kg" ; or, write as: " 0.6667 kg " .
__________________________________________
Step-by-step explanation:
__________________________________________
Basically, we can reduce the question to:
__________________________________________
What is " ¼" of "2 ⅔ kg" ?
_______________________________
→ (¼ * 2 ⅔) kg ; simplify the amount in "parentheses" ; & keep the units of "kg" (kilograms) ;
______________________________________________
Write " 2 ⅔ " as an "improper fraction" ;

→ To do so, multiply the "3" in the "denominator" (from the fraction, " ⅔ ") ;
by the "2" (from the whole number).

→ 3 * 2 = 6 .
_________________________________________

→ Then, take this value; in our case, "6" ; and the number "2" (from the "2" in the "numerator" (from the fraction portion, " ⅔ ").

→ 6 + 2 = 8 .
__________________________________________
→ Then, take this value, and write is as the "numerator" over a "new fraction" ; this "new fraction" is the: "improper fraction" . The "denominator" of this "new fraction" (i.e. "improper fraction") ; is the number from the "denominator" of the fraction portion of our [originally written "mixed number" ; which in our case is: "3" (from the fraction portion, " ⅔ ") .
___________________________________________
→ So, our mixed number, " 2 ⅔ " , can be written in the "improper fraction form" ; which is: " ⁸/₃ " .
___________________________________________
→ Put simply: " 2 ⅔ = [ (3*2) + 2 ] / 3 = (6 + 2) / 3 = 8/3 ; or, " ⁸/₃ " .
___________________________________________
→ We have: "(¼ * 2 ⅔) kg " .

→ Replace the: " 2 ⅔ " value with: " ⁸/₃ " ; to more easily simplify the expression in "parentheses" ; & to more easily solve the problem ;
__________________________________________________
→ "(¼ * 2 ⅔) =
`(1)/(4)`*
`(8)/(3)` " ;

= ? ;
___________________________________________________
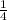→ We have: "
`(1)/(4)`*
`(8)/(3)` " ;

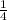→ The "4" can be 'canceled out' to a "1" ;
and the "8" can be 'canceled out', and changed to a "2" ;

→ since: "(8÷4=2)" ; and since: "(4÷4=1)" .
___________________________________________________
So now; we have: "
`(1)/(1)` *
`(2)/(3)` " ;
___________________________________________________
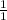→ The "
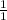`(1)/(1)` " can be eliminated;

→ since: "(1÷1=1)" ;
→ {Note that any value, divided by "1", is equal that same value ;
& that "any non-zero value", divided by "that same value", is equal to "1" .
______________________________________________________
→ As such: "
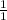`(1)/(1)` " = {1÷1} = 1 ;
& this value, which is "1", multiplied by [the other expression], will be equal to that other expression;
since:
______________________________________________________
→ [the other expression, which is a non-zero value] , multiplied by "1", is equal to [the SAME other expression, which is a non-zero value].
______________________________________________________
→ As such, we can completely eliminate the: "
`(1)/(1)` " ;

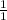and we are left with: " ⅔ " . The units are "kg" .

So; the answer is: " ⅔ kg" ;

Note: " ⅔ " = 2÷3 = 0.666666666666667 ;
____________________________________________
So; the answer is: " ⅔ kg" ; or, write as: 0.6667 kg .
____________________________________________