Question

The median of the values of the data set is h. If 625 were subtracted from each of the values in the data set what would be the median of the resulting data ?

A. H - 625
B.625 - h
C.h + 625
D.625 • h

Answer 1

Meanaverage:
add everything & divide by how manyMedianmiddle value (medium):
write data in order, find the middle value
if there are two middles, find their averageModemost frequent value:
find the number you see the most number of timesRangespread (or span) of the data:
max - min
subtract the maximum (biggest) value minus the minimum (smallest) valueVariationmeasures the spread of the data
(how far apart the data points are from the mean)Symmetrical Graphthe data is close together:
there is less difference from each data point to the mean valueNormal Distribution

Answer 2

Hi!

The correct answer is A. h-625.

Explanation:

If you have a dataset listed in ascending order:

`A = \lbrace\ a_1, a_2, a_3,..., a_(n)/(2),..., a_n \rbrace`

`median = a_(n)/(2)`

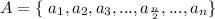
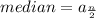
The value of the mean, if the dataset is even:

• The value of that divides a data sample into two halves.

The value of the mean, if the dataset is odd:

• The average of the two middle values that divide a data sample into two halves.

If we substract 625 to each value of the dataset:

`A = \lbrace\ a_1 - 625, a_2 - 625, a_3 - 625,..., a_(n)/(2) - 625,..., a_n - 625 \rbrace`

`median = a_(n)/(2) - 625`

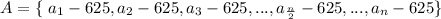
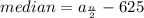
The position of the middle value is the same before the subtraction of 625, then the median would be H - 625.