Question

Given that the standard error of the sample proportion is 0.0195 and the point estimate follows a nearly normal distribution, calculate the test statistic (the z-statistic).

Answer 1

Given the question:

Nearsighted. It is believed that nearsightedness affects about 8% of all children. In a random sample of 194 children, 21 are nearsighted.

(a) Construct hypotheses appropriate for the following question: do these data provide evidence that the 8% value is inaccurate?

(b) What proportion of children in this sample are nearsighted?

(c) Given that the standard error of the sample proportion is 0.0195 and the point estimate follows a nearly normal distribution, calculate the test statistic (the Z-statistic).

(d) What is the p-value for this hypothesis test?

(e) What is the conclusion of the hypothesis test?

Part A:

The appropriate hypotheses for the question: do these data provide evidence that the 8% value is inaccurate is given by


`H_o:p=0.08 \\ \\ H_a:p\\eq0.08`



Part B:

The proportion of children in this sample that are nearsighted is given by


`(21)/(194) =0.1082=10.82\%`



Part C

Given that the standard error of the sample proportion is 0.0195 and the point estimate follows a nearly normal distribution,

The test statistic is calculated as follows:


`\frac{\hat{p}-p}{SE_p} = (0.1082-0.08)/(0.0195) = (0.0282)/(0.0195) =1.446`

Therefore, the test statistic is 1.446.



Part D

The p-value for this hypothesis test is given by


`P(-1.446 \leq z \leq 1.446)=2P(z\leq-1.446)=2(0.0741)=0.1482`



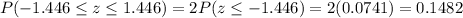
Part E

Since the P-value (0.1482) is relatively large, we cannot reject the null hypothesis.

Therefore, we conclude that these data does not provide evidence that the 8% value is inaccurate.