Question

Point M is the midpoint of AB . AM= 3x+3, and AB=8x−6

What is the length of AM?


The answer is 21 but i don't know the steps to get it. HELP

Answer 1

AM= Half of AB

or, 3x+3=(8x-6)/2
or, 6x+6=8x-6
or, 2x=12
Therefore,x=6

so,AM=3*6+3=21

Answer 2

The length of AM is:

21 units.

Explanation:

Point M is the midpoint of AB.

AM= 3x+3, and AB=8x−6

Since, the midpoint divides the line segment into two equal parts i.e. it bisects the line segment.

Hence, we have:

AM+MB=AB

Also, AM=MB

Hence, we have:

`3x+3+3x+3=8x-6`

on combining the like terms in the left hand side of the equation we have:

`3x+3x+3+3=8x-6\\\\6x+6=8x-6`

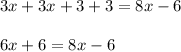
Now, on subtracting both side of the equation by 6x we have:

`6=8x-6-6x\\\\6=8x-6x-6\\\\6=2x-6`

on adding 6 on both side of the equation we have:

`6+6=2x\\\\12=2x\\\\2x=12\\\\x=(12)/(2)\\\\x=6`

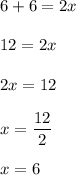
Hence, we have:

`AM=3* 6+3\\\\AM=21\ \text{units}`