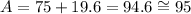Question

The figure below shows two half-circles at the ends of a rectangle with the dimensions shown calculate the total area of the figure Round your answer to the nearest whole number

Answer 1

95 square inches

Explanation:

The area of the figure would be the sum between the area of the rectangle and the area of the two semicircles, which in total would be that of the complete circle.

For the rectangle:

`\begin{gathered} A=l\cdot w=15\cdot5 \\ A=75 \end{gathered}`

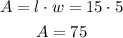
For the circle:

In the case of the circle, they give us the diameter that is equal to 5, but we need the radius, we know that the radius is equal to half the radius, therefore it would be like this:

`\begin{gathered} r=(d)/(2)=(5)/(2) \\ r=2.5 \\ \text{The area is:} \\ A=\pi\cdot r^2=3.14\cdot2.5^2 \\ A=19.6 \end{gathered}`

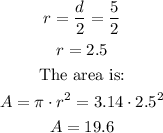
Now the total area would be:;

`A=75+19.6=94.6\cong95`