Question

What are the domain and range of g of x equals 3 times the square root of the quantity x plus 4?A. D: [3, ∞) and R: [0, ∞)B. D: [4, ∞) and R: (–∞, 0)C. D: [–4, ∞) and R: [0, ∞)D. D: (3, ∞) and R: (–∞, 0)

Answer 1

`\begin{equation*} D:\lbrack-4,\infty)\text{ and R:}\lbrack0,\infty) \end{equation*}`

Step-by-step explanation

given

`g(x)=3√(x+4)`

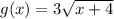
Step 1

Step 1

Domain.

The domain of a function is the set of values that we are allowed to plug into our function, in the case of square roots we need positive numbers ( greater or equal than zero) inside the symbols

so,

`\begin{gathered} √(x+4) \\ x+4\text{ must be grater or equal than 0} \\ x+4\ge0 \\ to\text{ solve for x, subtract 4 in both sides } \\ x+4-4\geqslant0-4 \\ x\ge-4 \end{gathered}`

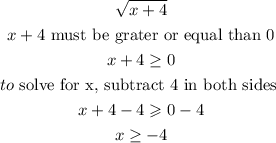
so, the x values must be greater or equal than -4, in set notation it is

`\lbrack-4,\infty)`

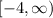
Step 2

The range of a function refers to the entire set of all possible output values of the dependent variable.

so, we know that for the root the outputs are equal or greater than zero, hence the function g(x) would be.

`\begin{gathered} g(x)=3√(x+4) \\ (√(x+4))\text{ will always be greater or equal than zero, so} \\ g(x)n\text{ will be 3 times that values} \\ so\text{ } \\ 3*(range\text{ \rparen} \\ 3*\lbrack0,\infty) \\ \lbrack0,\infty) \end{gathered}`

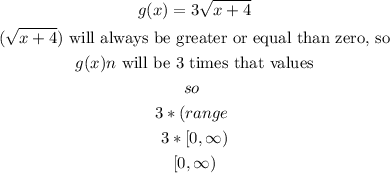
therefore, Range

`\lbrack0,\infty)`

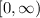
so, the answer is

`D:\lbrack-4,\infty)\text{ and R:}\lbrack0,\infty)`

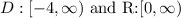
I hope this helps you