Question

PLEASE HELP ME. NO ONE IS HELPING ME. I AM SO CONFUSED. MY TEACHERS AND MY PARENTS WONT HELP ME EITHER.

Factor over the expression over the complex numbers.
x^2+20

Factor over the expression over the complex numbers.
x^2+36

Factor over the expression over the complex numbers.
x^4-81

Factor over the expression over the complex numbers.
y^4+14y^2+49

Factor over the expression over the complex numbers.
y^2+2y^2+16y+32

Answer 1

Problem 1


`x^2+20 = (x)^2 + \left(√(20)\right)^2`

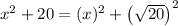
We have a sum of squares in the form a^2 + b^2 where

a = x
b = sqrt(20)

It turns out that

a^2 + b^2 = (a+bi)*(a-bi)

where i is the square root of negative 1

`i=√(-1)`

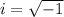
So this means,

`x^2+20 = (x)^2 + \left(√(20)\right)^2`


`x^2+20 = \left(x+√(20)*i\right)\left(x-√(20)*i\right)`

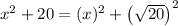
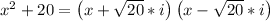
Answer:
`\left(x+√(20)*i\right)\left(x-√(20)*i\right)`

========================================

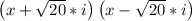
Problem 2

Similar to problem 1, we use the formula
a^2 + b^2 = (a+bi)*(a-bi)

In this case,
a = x
b = 6

So,

a^2 + b^2 = (a+bi)*(a-bi)
x^2 + 6^2 = (x+6i)*(x-6i)
x^2 + 36 = (x+6i)*(x-6i)

Answer: (x+6i)*(x-6i)

========================================

Problem 3

Use the difference of squares rule twice to get

x^4 - 81 = (x^2)^2 - (9)^2
x^4 - 81 = (x^2-9)(x^2+9)
x^4 - 81 = (x^2-3^2)(x^2+9)
x^4 - 81 = (x-3)(x+3)(x^2+9)
x^4 - 81 = (x-3)(x+3)(x^2+3^2)
x^4 - 81 = (x-3)(x+3)(x-3i)(x+3i)

Answer: (x-3)(x+3)(x-3i)(x+3i)

========================================

Problem 4

This is in the form a^2 + 2*a*b + b^2 where
a = y^2
b = 7

So,

`a^2 + 2*a*b + b^2 = (a+b)^2`


`(y^2)^2 + 2*(y^2)*7 + 7^2 = (y^2+7)^2`


`y^4 + 14y^2 + 49 = (y^2+7)^2`


`y^4 + 14y^2 + 49 = (y^2+(√(7))^2)^2`


`y^4 + 14y^2 + 49 = ((y-√(7))(y+√(7)))^2`

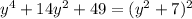
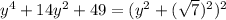
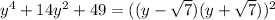
Answer:
`y^4 + 14y^2 + 49 = ((y-√(7))(y+√(7)))^2`

========================================

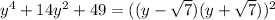
Problem 5

I'm assuming the expression should be y^3+2y^2+16y+32

Use factoring by grouping

y^3+2y^2+16y+32
(y^3+2y^2)+(16y+32)
y^2(y+2)+(16y+32)
y^2(y+2)+16(y+2)
(y^2+16)(y+2)
(y^2+4^2)(y+2)
(y-4i)(y+4i)(y+2)

Answer: (y-4i)(y+4i)(y+2)