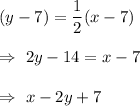Answer:

Explanation:
Given : The line
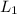 has equation
has equation
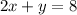
In intercept form :

The slope of
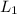 =-2 [in intercept form equation of line
=-2 [in intercept form equation of line
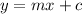 , m is slope ]
, m is slope ]
Let p be slope of
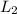
We know that when two lines are perpendicular then the product of their slopes is -1.
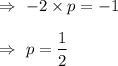
The equation of line having slope 'm' and passing through (a,b) is given by :-
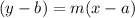
Then , equation of line
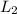 will be :-
will be :-