Question

A farmer has 260 feet of fencing to make a rectangular corral. What dimensions will make a corral with the maximum area? What is the maximum area possible?

Answer 1

Suppose we have a rectangle with a side of length L and another side of length (L-x). The area of the rectangle is

`A=L(x-L)=Lx-L^2`
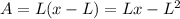
We impose the condition of maximum

`dA/dL =0`
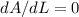
Thus
`x-2L=0`

`x=2L`
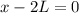
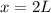
Hence the maximum area is when we have a square

`A =L(2L-L) =L^2`
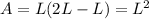
With a perimeter
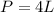
`P=4L` we obtain
`L=P/4 =260/4=65 feet`
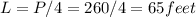
which gives A =L^2=65*65 =6225 ft^2