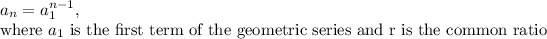Answer:
Option D)
Common ration =
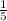 = 0.2
= 0.2
The next three terms of the given series are: 0.08, 0.016, 0.0032
Explanation:
We are given the following information in the question:
We are given a geometric sequence:
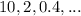
Geometric Series
- A geometric series is a series with a constant ratio between successive terms
We have to find the common ration of the given geometric series:
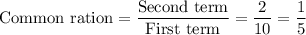
The
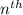 term of a geometric sequence is given by:
term of a geometric sequence is given by:
Formula: