Part (i)
We can use the slope formula on the points A(0,4) and C(8,0)
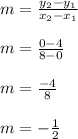
The slope of line AC is -1/2.
Line BM is perpendicular to AC. This indicates we'll apply the negative reciprocal to -1/2 to end up with 2.
The slope of line BM is 2.
Note that the perpendicular slopes multiply to -1. This is true of any perpendicular pair of slopes as long as neither line is vertical nor horizontal.
Answers:
- Slope of line AC = -1/2
- Slope of line BM = 2
=============================================================
Part (ii)
The slope of
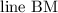 was m = 2 from the previous part above.
was m = 2 from the previous part above.
We'll use the coordinates of point B(9,7) along with this slope value to find the equation of
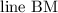 .
.
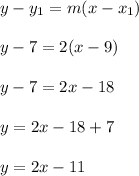
Answer: y = 2x-11
=============================================================
Part (iii)
The equations for lines
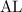 and
and
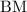 are
are
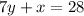 and
and
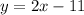 in that order. Solving this system of equations will produce the location of point P, where the lines intersect.
in that order. Solving this system of equations will produce the location of point P, where the lines intersect.
Let's apply substitution to solve for x.
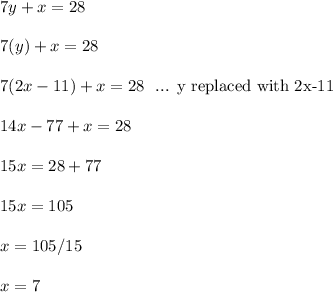
Then use this to find the y coordinate.
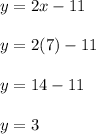
The location of point P is (7,3). This is the orthocenter of the triangle where the altitudes intersect.
Answer: (7,3)