Answer:
The pair which are inverse of each other are:
Option: C
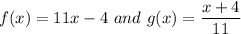
Explanation:
Two functions f(x) and g(x) are said to be inverse of each other if:
fog(x)=gof(x)=x
i.e. the composition of two functions give identity no matter what the order is.
A)
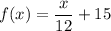 and
and

Now we calculate fog(x):
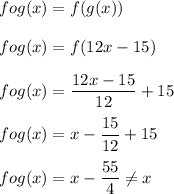
Hence, option: A is incorrect.
B)

Now we calculate fog(x):

Hence, option: B is incorrect.
D)
![f(x)=9+\sqrt[3]{x}\ and\ g(x)=9-x^3](https://img.qammunity.org/2018/formulas/mathematics/high-school/vlvfi93oy4lw94d8wcph37iuvtmwpmqukt.png)
Now we calculate fog(x):
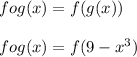
![fog(x)=9+\sqrt[3]{9-x^3}\\eq x](https://img.qammunity.org/2018/formulas/mathematics/high-school/2yx2calrm2oqxb689r20ia7kq0tvdtfwo5.png)
Hence, option: D is incorrect.
C)
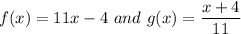
Now we calculate fog(x):
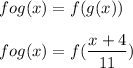
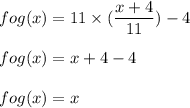
Similarly,
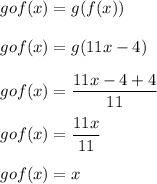
Hence, option: C is the correct option.