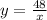Question

When x = 3, y = 16 and when x = 6, y = 8. Which inverse variation equation can be used to model this function? y = y = 48x y = y =

Answer 1

Y=48/x hope this helps you

Answer 2

`y = (48)/(x)`

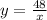
Explanation:

Inverse variation:

if
`y \propto (1)/(x)`

then the equation is in the form of:

`y = (k)/(x)` ....[1]

where, k is the constant of variation.

As per the statement:

When x = 3, y = 16 and when x = 6, y = 8.

Substitute the value of x and y to find k.

Case 1.

When x = 3, y = 16

then;

`16=(k)/(3)`

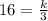
Multiply by 3 both sides we have;

48 = k

or

k = 48

Case 2.

When x = 6, y = 8

then;

`8=(k)/(6)`

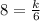
Multiply by 6 both sides we have;

48 = k

or

k = 48

In both cases, we get constant of variation(k) = 48

then the equation we get,

`y = (48)/(x)`

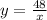
Therefore, the inverse variation equation can be used to model this function is,
`y = (48)/(x)`