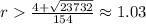Question

The area of a rectangular rug is given by the trinomial r squared minus 4 r minus 77r2−4r−77. What are the possible dimensions of the​ rug? Use factoring.

Answer 1

r2-4r-77 = (r-11)(r+7)
r has to be greater than 11 in order for the formula to represent the area of a rug since a side length cannot be less than or equal to 0.

Answer 2

`r>(4 +√(23732) )/(154) \approx1.03\\`

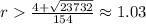
Explanation:

The area of the rectangular rug is given by this equation:

`77r^2-4r-77`

The area must be a number greater than 0 since a negative area, or an area equal to 0 wouldn't have much sense. So:

`77r^2-4r-77>0`

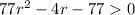
Let's find the roots of this equation using the quadratic formula:

`r=(-b\pm √(b^2-4ac) )/(2a) =(-(-4)\pm√((-4)^2-(4)(77)(-77)) )/(2(77)) \\\\r=(4 \pm √(23732) )/(154) \\\\r_1=(4 +√(23732) )/(154) \approx1.03\\\\r_2=(4 - √(23732) )/(154) \approx-0.97`

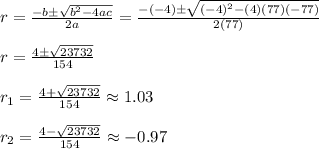
Now, let's evaluate the area for
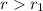`r>r_1` for example r=1.05:

`A=77(1.05)^2-4(1.05)-77=3.6925>0`

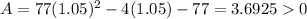
The result is greater than zero, so for
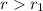`r>r_1` the values make sense.

Now let's evaluate the area for
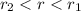`r_2<r<r_1` for example r=0.5 and r=-0.7:

`A=77(0.5)^2-4(0.5)-77=-59.75<0\\\\A=77(-0.7)^2-4(-0.7)-77=-36.47<0`

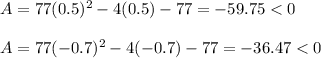
The result is less than zero, so for
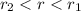`r_2<r<r_1` the values don't make sense.

Now, let's evaluate the area for
`r<r_2` for example r=-1:

`A=77(-1)^2-4(-1)-77=4>0`

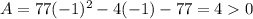
The result is greater than zero, so for
`r<r_2` the values make sense

However, since negative values of r wouldn't make much sense (I never heard about of -8 inches for example) the possible dimensions of the​ rug are just:

`r>(4 +√(23732) )/(154) \approx1.03\\`